Monte Carlo

Questions
  • How do I generate random numbers?
  • How do I integrate using Monte Carlo methods?
  • When might Monte Carlo integration be useful?
Objectives
  • Use the random module to generate random numbers
  • Use Monte Carlo methods to calculate the area of a circle

There are many different numerical methods for calculating integrals

In the previous section we studied the simplest methods for calculating integrals: the rectangular-slice method . For increased accuracy and computational efficiency, there are extensions to this approach - for example, the trapezoid method (where each slice is a trapezoid rather than rectangle) or Simpson’s rule (where a quadratic curve is fitted to each slice). For certain classes of functions we can increase the performance further using more specialised approaches such as Gaussian Quadrature.

One particularly flexible and general purpose approach for calculating integrals is to use Monte Carlo integration. This approach is useful when the integrand is “pathological” (wildly varying) or noisy, or when the integration is performed over several variables.

Monte Carlo methods calculate the answers to exact calculations by doing random calculations

Monte Carlo methods are a broad class of algorithms that rely on random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. “Monte Carlo” is a reference to a well-known casino town, since the element of chance is core to the modelling approach, similar to various casino games.

Monte Carlo methods are applied across a wide variety of domains, most commonly mathematics, physics and finance. In physics, Monte Carlo methods are used to design particle detectors, model galaxy evolution and solve the many-body problem for quantum systems, amongst many other applications. In this lesson we will introduce one of the main uses of Monte Carlo: for integration.

The Monte Carlo “area method” estimates integrals by generating a uniform sample of points and counting how many fall into a planar region

Consider the shaded area as shown below. This is the integral \(I\) which we wish to calculate.

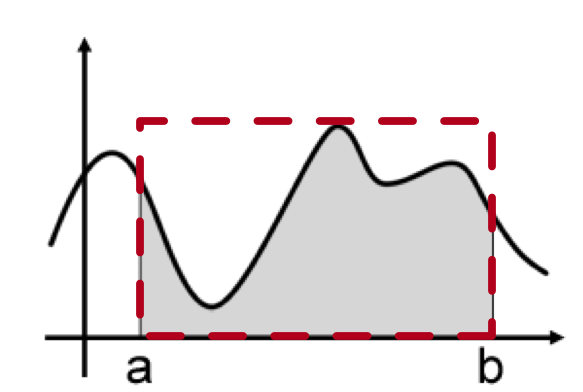
If we choose a point uniformly at random in the rectange (dashed red line) that bounds the shaded area, the probability \(p\) that the point falls in the shaded area is

\[p = \frac{I}{A}\]

where \(A\) is the area of the bounding rectangle. This means that the integral \(I\) can be calculated if we know the area of the bounding rectangle and the probability \(p\):

\[I = Ap\]

To calculate \(p\) we can randomly generate \(N\) points in the bounding area and keep count as to how many lie in the shaded area. If \(k\) lie in the shaded area then the fraction of points \(\frac{k}{N}\) should be equal to the probability \(p\).

\[I = \frac{Ak}{N}\]

We can extend this approach to higher dimensions to consider integrands lying within a bounding volume, or higher dimensional space (which is considered in the extension exercise for this lesson).

We can use the Monte Carlo area method to estimate pi

We’ll now use this approach to give us an estimate for the value of pi by considering the area under a quarter-circle.

The relevant equations are:

square area: \(A_s = (2 r)^2\)
circle area: \(A_c = \pi r^2\)

The ratio of the areas can be related to \(\pi\) through the following expressions:

\[\frac{A_c}{A_s} = \frac{\pi r^2}{4 r^2} = \frac{\pi}{4}\]
\[\pi = 4\frac{A_c}{A_s}\]

To approximate the ratio \(\frac{A_c}{A_s}\) we will generate a (uniform) pseudo-random number between 0 and 1 for our x-coordinates, and a (uniform) pseudo-random number between 0 and 1 for our y-coordinates. We will then check if our random point lies in or out of the circle. The probability \(P_i\) that our point lies in the circle is related to the area ratio and so value of pi:

\[P_i = \frac{A_c}{A_s} = \frac{\pi}{4}\]

The Monte Carlo area method can be translated into Python code

# importing the modules we will need
import random
import math

# in this function we generate random numbers and count how many lie within the circle
def estimate_pi(num_points):
    
    points = []
    hits = 0
    for i in range(num_points):
        # random.random returns a random number drawn from a uniform distribution from 0 to 1
        x, y = random.random(), random.random()
        # we test if the point is within the circle (using the equation for a circle, X^2+y^2=r^2)
        if x*x + y*y < 1.0:
            hits += 1
    
    probability = hits / num_points
    return probability*4
        
estimate_pi(1000)
3.104
estimate_pi(2000)
3.176

This method usually improves with the number of points, however there can be some variation due to the randomness of the numbers used. If you would like others to reproduce your exact results, you can seed the (pseudo-)random number generator:

random.seed(1)
print("error is {}".format(math.pi-estimate_pi(1000)))
error is 0.029592653589793017
random.seed(1)
print("error is {}".format(math.pi-estimate_pi(2000)))
error is -0.004407346410206792

Monte Carlo integration is computationally efficient for particular types of integrand

The error when using Monte Carlo integration is proportional to \(N^{-\frac{1}{2}}\), which is larger than the rectangular slice approach with error order \(h \propto N^{-1}\) (where \(N\) in this case is the number of integration slices). However Monte Carlo methods are more flexible and can be used where other methods break-down: for example, they are particularly useful for integrating functions where the integrand varies very quickly, and/or where the integral is over many variables. In many cases, for “well behaved” functions, an approach based on Riemann summation will give more accurate and computationally efficient results.

Keypoints
  • There are many different numerical methods for calculating integrals
  • Monte Carlo methods calculate the answers to exact calculations by doing random calculations
  • The Monte Carlo “area method” estimates integrals by generating a uniform sample of points and counting how many fall into a planar region
  • We can use the Monte Carlo area method to estimate pi
  • The Monte Carlo area method can be translated into Python code
  • Monte Carlo integration is computationally efficient for particular types of integrand

Test your understanding

  1. Use Monte Carlo integration (with 100 random points) to calculate the value of the integral:

\[ I = \int_{-1}^1\sqrt{1-x^2}\mathrm{d}x \]

  1. How does this compare to exact answer? (Hint: the integrand is a semicircle of radius 1)

  2. How can you improve the accuracy of your estimate?

  3. Increase the number of points until you get an accuracy comparable (same order of magnitude) as the Riemann sum method with 100 points.

  4. Use the %%timeit notebook magic to compare the calculation times for the Riemann sum method and Monte Carlo method. Which is more efficient?

  1. We want to calculate the area of a semicircle with radius 1. We can adapt the approach used in the Monte Carlo tutorial but, in this case, we use the fact that \(P_i = \frac{A_c}{A_r}\) where \(A_r\) is a rectangle of length 2 (as the semicircle goes from \(-1\) to \(1\)) and height 1.
import random
import math
    
def estimate_semicircle_area(num_points):
    
    points = []
    hits = 0
    for i in range(num_points):
        # random.uniform(a,b) returns a random number drawn from a uniform distribution from a to b
        x, y = random.uniform(-1,1), random.uniform(0,1)
        # we test if the point is within the circle (using the equation for a circle, X^2+y^2=r^2)
        if x*x + y*y < 1.0:
            hits += 1
    
    probability = hits / num_points
    rectangle_area = 2
    return probability*rectangle_area
    
estimate_semicircle_area(100)
1.58

Note that your estimate will be different as you be using a different set of random numbers.

  1. The exact answer is \(\frac{\pi}{2}\). The error on our calculation is
math.pi/2 - estimate_semicircle_area(100)
-0.04920367320510355
  1. To improve the accuracy we can use a larger number of random points:
math.pi/2 - estimate_semicircle_area(1000)
0.04679632679489654
math.pi/2 - estimate_semicircle_area(10000)
-0.0048036732051033315

  1. Increasing the number of points to 10,000 gives an error comparable to the Riemann sum method with 100 integration slices (where the error is 0.002).

  2. Let’s use the %%timeit magic to time how long each takes to run

%%timeit
estimate_semicircle_area(10000)
6.23 ms ± 370 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%%timeit
rectangular_slice_integral(semicircle, -1, 1, 100)
31 µs ± 1.09 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

As each method gives roughly the same accuracy, but the estimate_semicircle_area is 100x smaller, we can deduce that the Monte Carlo method implemented in estimate_semicircle_area is considerably less efficient than the Riemann summation method implemented in rectangular_slice_integral. However the Monte Carlo method is useful for badly behaving systems, as we will see in the lesson exercises.