Initial and boundary conditions
PDEs can have boundary conditions and initial conditions
In the previous section of the course we learnt that ODEs have either initial values or boundary values.
Boundary value problems
PDEs can also be separated in a similar manner. Boundary value problems describe the behaviour of a variable in a space and we are given some constraints on the variable around the boundary of that space. For example, consider the 2-dimensional problem of a thin rectangular sheet with one side at voltage \(V\) and all others at voltage zero.
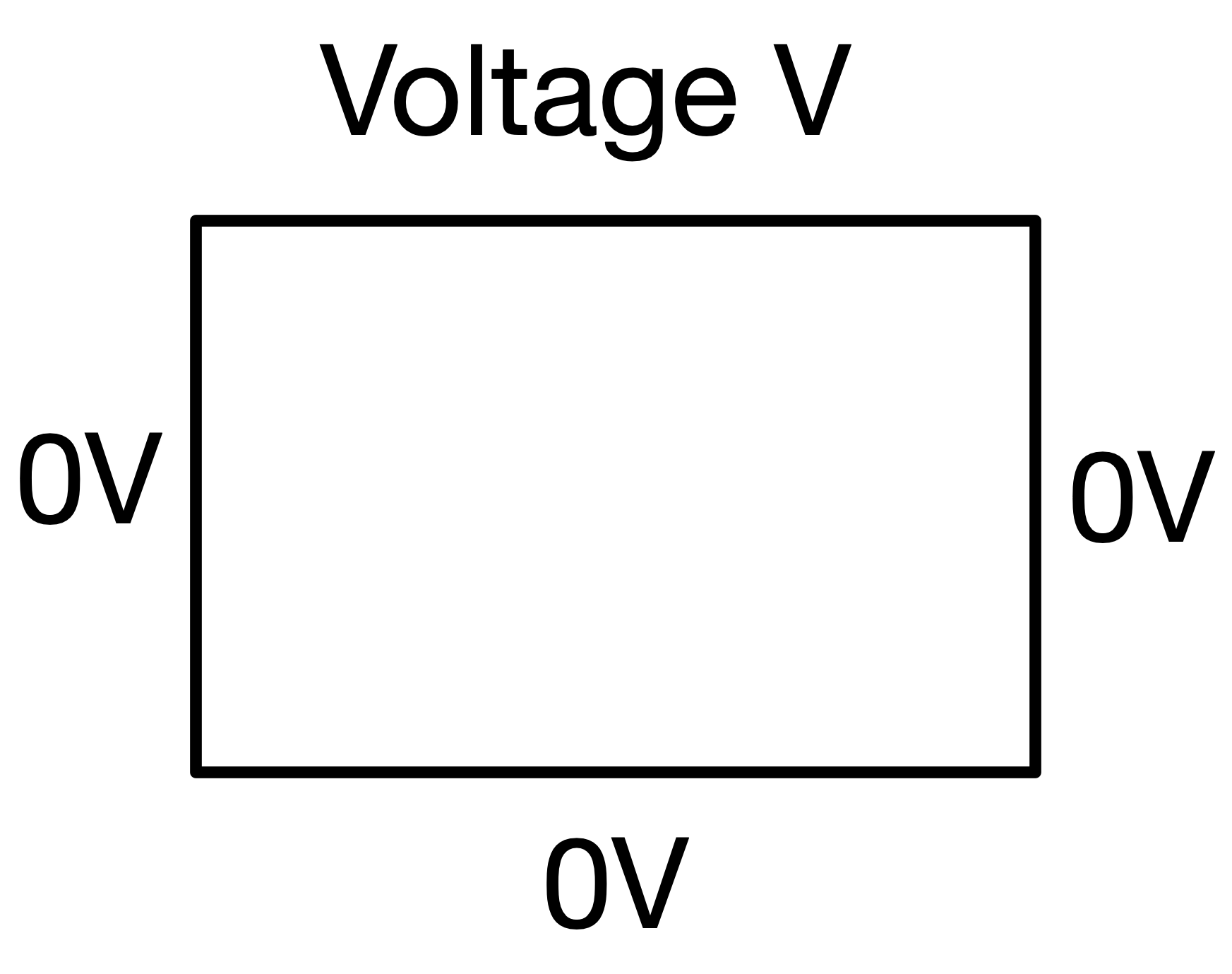
The specification that one side is at voltage \(V\) and all others are at voltage zero are the boundary conditions. We could then calculate the electrostatic potential \(\phi\) at all points within the sheet using the two-dimensional Laplace’s equation:
\[\begin{equation} \nabla^2\phi = \frac{\partial^2\phi}{\partial x^2} + \frac{\partial^2\phi}{\partial y^2} = 0 \end{equation}\]
Initial value problems
Initial value problems are where the field - or other variable of interest - is varying in both space and time. We now require boundary conditions and initial values. This is a more difficult type of PDE to solve.
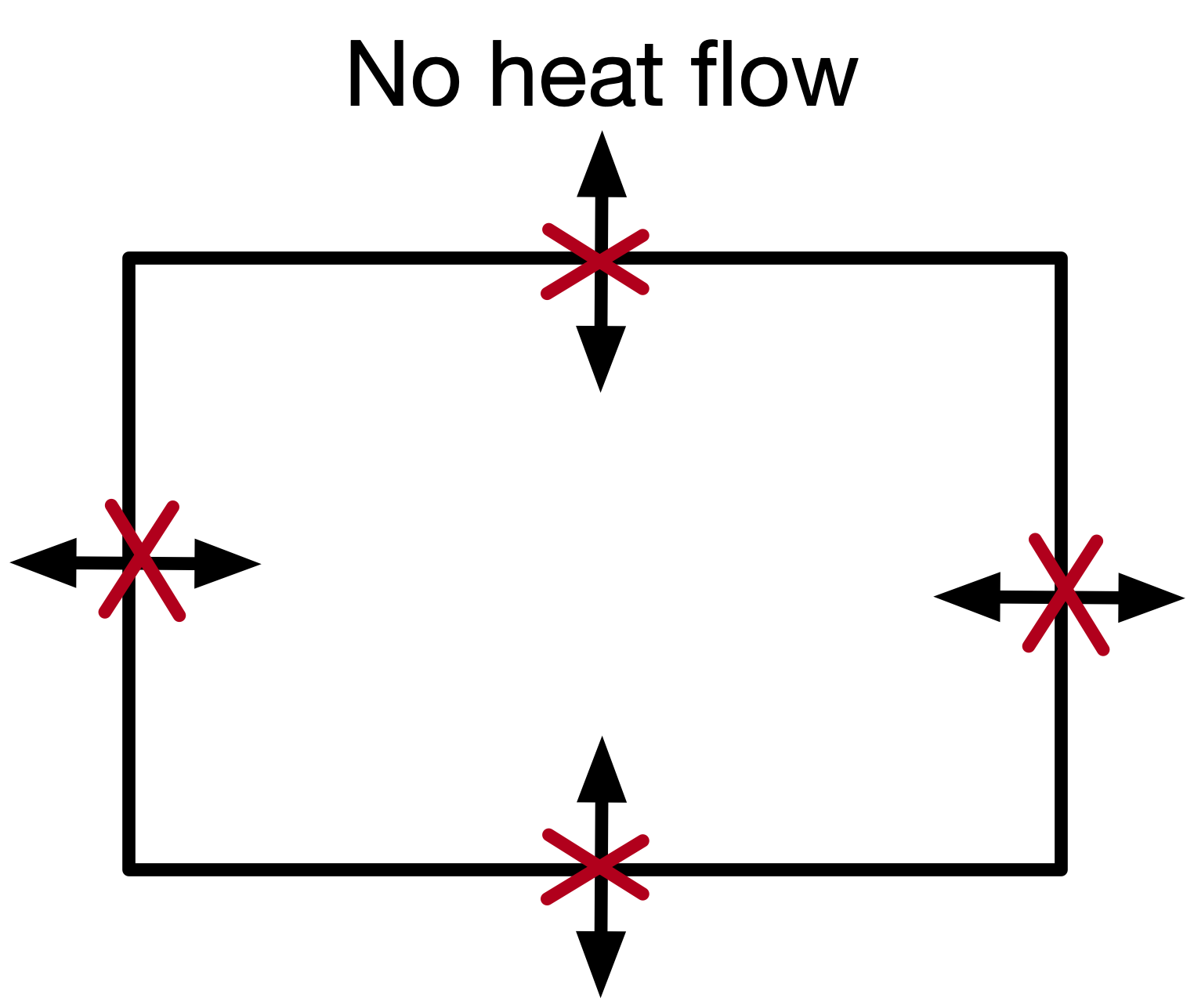
For example, consider heat diffusion in a two-dimensional sheet. Here we could specify that there is no heat flow in or out of the sheet - this is the boundary condition.
We could also specify that at time \(t=0\) the centre of the sheet is at temperature \(T_1\), whilst surrounding areas are at temperature \(T_0\). This is the initial condition. It differs from a boundary condition in that we are told what the temperature is at the start of our time grid (at \(t=0\)) but not at the end of our time grid (when the simulation finishes).
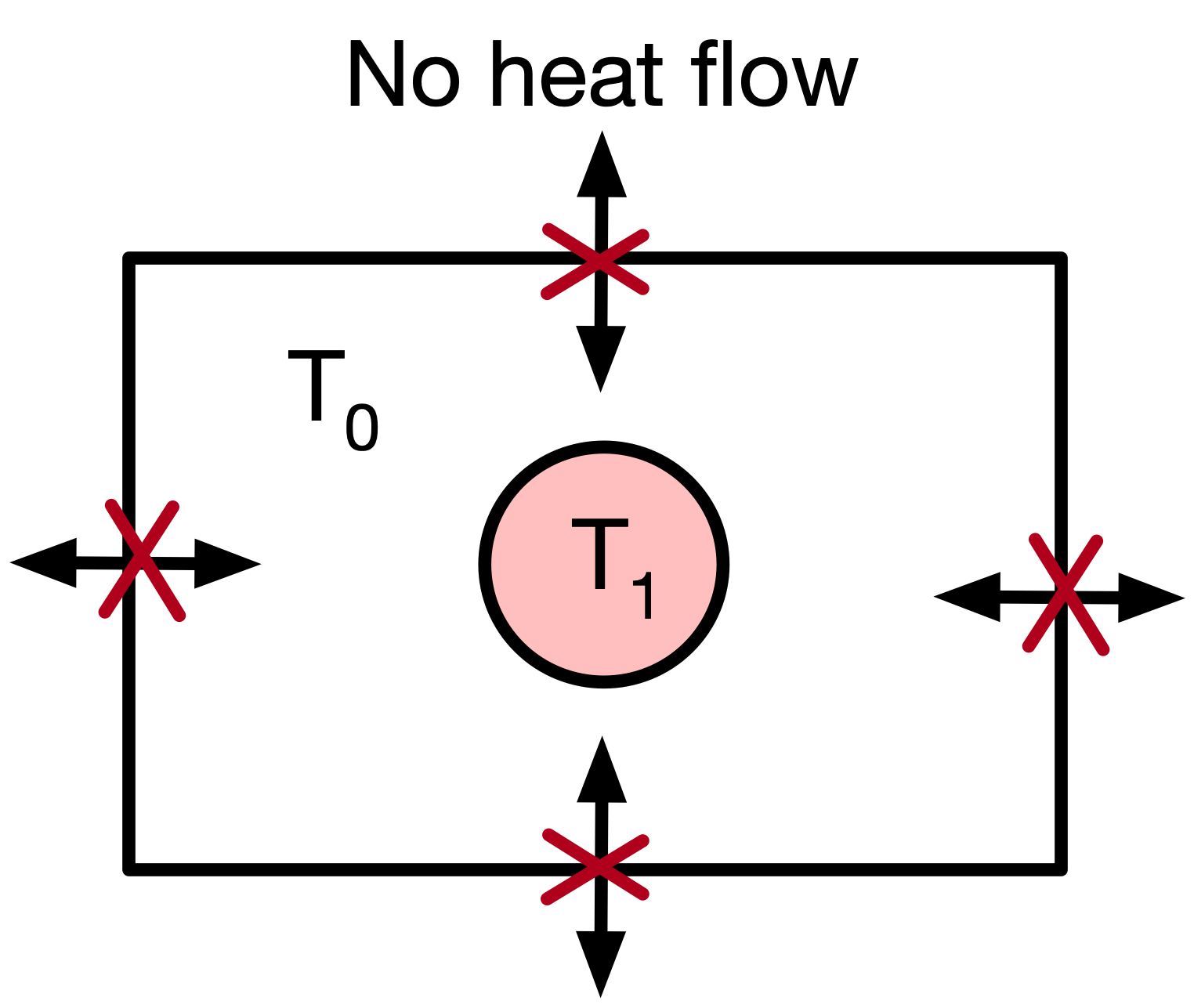
We could then calculate the temperature at time \(t\) at all points \([x,y]\) within the sheet using the two-dimensional Diffusion equation:
\[\begin{equation} \nabla^2T = \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2}=\alpha \frac{\partial T}{\partial t} \end{equation}\]